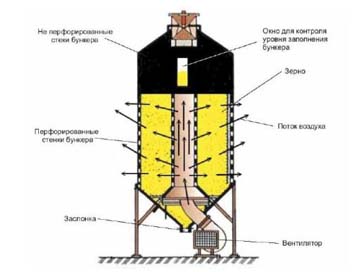
При термической сушке кинетика внешнего тепломассообмена определяется изменением температуры агента сушки около поверхности влажного материала и изменением концентрации влажных паров поперек пограничного слоя. Подвод тепла к влажному материалу обеспечивается за счет разности температур между основным слоем агента сушки и поверхностью этого материала. За счет разницы концентраций образуется поток пара от поверхности.
На сегодняшний день очень сложно аналитически рассмотреть внешнюю задачу тепломассообмена в процессе сушки с учетом многочисленных факторов, оказывающих на это влияние, из-за сложности определения движущих сил процессов сушки и кинетических коэффициентов.
В теории сушки для анализа внешнего тепломассообмена применяется метод, в основу которого положено рассмотрение уравнений неразрывности и движения вязкого несжимаемого потока:
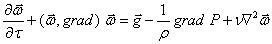 |
(1.1) |
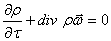 |
(1.2) |
конвективно-диффузинного переноса влажных паров в агенте сушки
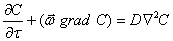 |
(1.3) |
и уравнения, которым описывается температурное поле в потоке теплоносителя
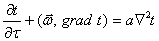 , , |
(1.4) |
где ![]() , Р, С, t – функции скорости, статического давления, концентрации влаги и температуры в потоке агента сушки;
, Р, С, t – функции скорости, статического давления, концентрации влаги и температуры в потоке агента сушки; 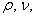 а и D – это плотность, коэффициенты вязкости, температуропроводности и диффузии паров в сушильном агенте; g – ускорение свободного падения;
а и D – это плотность, коэффициенты вязкости, температуропроводности и диффузии паров в сушильном агенте; g – ускорение свободного падения;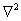 - оператор Лапласа;
- оператор Лапласа;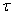 - время.
- время.
Влияние процессов переноса теплоты, импульса и массы друг на друга в представленной системе уравнений (1.1) – (1.4) учитывается зависимостью кинетических коэффициентов от потенциалов переноса.
Представленные уравнения оказываются справедливыми как для ламинарного, так и турбулентного течения, при условии, что локальные значения функций P, t,![]() , C понимаются как усредненные во времени, а коэффициенты D, a и
, C понимаются как усредненные во времени, а коэффициенты D, a и 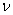 состоящими каждый из нескольких слагаемых – турбулентного и молекулярного коэффициентов переноса массы, теплоты и импульса.
состоящими каждый из нескольких слагаемых – турбулентного и молекулярного коэффициентов переноса массы, теплоты и импульса.
Благодаря теории пограничного слоя можно существенно упростить эту систему уравнений. Но и при этом теоретически решаются только самые простые задачи для изотермических условий обтекания тел с малой кривизной.
Анализ внешнего тепломассобмена с помощью теоретических методов сложен и заставляет использовать для этого экспериментальные данные.
При непосредственных измерениях установлено формирование нескольких пограничных слоев около влажной поверхности материала. Это концентрационный, гидродинамический слой и тепловой. Для общих случаев не было отмечено подобие полей скорости, влагосодержания и температуры теплоносителя около той же влажной поверхности материала.
Опытные данные интенсивности процессов массообмена и теплообмена поверхности материала с сушильным агентом приводятся в виде зависимости критериев подобия, получаемых из уравнений (1.1.) – (1.4), и условий однозначности. Главное условие записывается в виде уравнения конвективной массоотдачи, где содержится соответствующий коэффициент массоотдачи 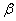 , по значению которого можно судить об интенсивности массообмена поверхности материала с сушильным агентом.
, по значению которого можно судить об интенсивности массообмена поверхности материала с сушильным агентом.
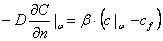 |
(1.5) |
В этом уравнении концентрация влаги в агенте сушки 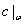 и градиента концентраций
и градиента концентраций 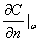 по нормали к поверхности выбираются на самой поверхности влажного материала.
по нормали к поверхности выбираются на самой поверхности влажного материала.
Для принудительного движения воздушного потока относительно поверхности материала составлено критериальное выражение теплообмена:
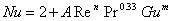 |
(1.6) |
где Nu=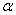 d/
d/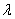 - критерий Нуссельта; Gu=(T-Tм)/T – параметрический критерий; Т-температура воздуха, Тм – температура адиабатического насыщения; d – характерный размер тела;
- критерий Нуссельта; Gu=(T-Tм)/T – параметрический критерий; Т-температура воздуха, Тм – температура адиабатического насыщения; d – характерный размер тела; 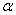 - коэффициент теплоотдачи;
- коэффициент теплоотдачи; 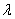 - коэффициент теплопроводности агента сушки.
- коэффициент теплопроводности агента сушки.
Когда Re>200, то постоянным слагаемым в представленном уравнении пренебрегают.
Уравнение для массообменного критерия Нуссельта выглядит так:
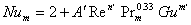 |
(1.7) |
Значения параметров из уравнений (1.6) и (1.7) приведены ниже. Они зависят от диапазона изменений Re.
Приведенные уравнения (1.6) и (1.7) применяются для установления интенсивности процессов теплообмена и массообмена между твердым телом, поверхность которого во время сушки влажная, и сушильным агентом. Нужно учесть следующее: в процессе испарении влаги со временем достигается состояние, когда из внутренних зон влага подводится медленнее, чем она убывает с поверхности. Из-за этого температура на поверхности возрастает; внутри капиллярно-пористого тела влага превращается в пар. Количество паров, которые проходят поперек пограничного слоя, становится меньше, поэтому и меняются коэффициенты теплоотдачи и массоотдачи от поверхности. Изменение теплоотдачи, которое зависит от изменяющегося в меньшую сторону влагосодержания материала, учитывается симплексом U/Uкр. В данном случае Uкр – это критическое значение влагосодержания. При нем скорость сушки перестает быть постоянной, а поверхность материала уже не полностью смоченная. Степень воздействия этого соотношения на значение Nu зависит от строения тела и формы связи влаги с материалом.
Исследования зависимости обсуждаемых коэффициентов 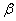 и
и 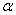 от влагосодержания материала осложняются в реальности тем, что тела имеют неоднородную структуру, поэтому есть участки с неравномерным распределением влаги по поверхности, что является причиной различных значений коэффициентов на поверхности материала. Эти коэффициенты так же меняют свои значения из-за гидродинамических условий обтекания разных участков на поверхности. В связи с этим опытные данные представляют с усредненными значениями коэффициентов тепло- и массообмена.
от влагосодержания материала осложняются в реальности тем, что тела имеют неоднородную структуру, поэтому есть участки с неравномерным распределением влаги по поверхности, что является причиной различных значений коэффициентов на поверхности материала. Эти коэффициенты так же меняют свои значения из-за гидродинамических условий обтекания разных участков на поверхности. В связи с этим опытные данные представляют с усредненными значениями коэффициентов тепло- и массообмена.
При испарении влаги в вынужденный воздушный поток со сферических поверхностей с разными диаметрами было получено уравнение для коэффициентов массоотдачи:
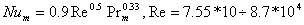 |
(1.8) |
Есть и еще одна формула, которая более сложная, но, по мнению авторов этой работы, она учитывает вклад в массообмен кормовой и передней частей сферы. Эта формула справедлива для большого диапазона Re:
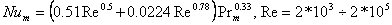 |
(1.9) |
Существует и еще ряд аппроксимационных выражений. Например, для диапазона 10<Re<105 с относительно небольшой погрешностью (20%) справедлива корреляция, которая почти совпадает с уравнением (1.8). Для естественной конвекции в интервале GrmPrm=106?1010
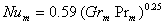 |
(1.10) |
в критерии Грасгофа 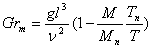 учитываются средние мольные массы паровоздушной смеси у поверхности испарения и в объеме сушильного агента (Mn и М) и температуры у поверхности продукта и массы среды (Тn, Т). l – это определяющий размер, за который взята длина обтекания тела. В случае плоской поверхности принимается длина в направлении потока, а для шара или цилиндра она рассчитывается l=
учитываются средние мольные массы паровоздушной смеси у поверхности испарения и в объеме сушильного агента (Mn и М) и температуры у поверхности продукта и массы среды (Тn, Т). l – это определяющий размер, за который взята длина обтекания тела. В случае плоской поверхности принимается длина в направлении потока, а для шара или цилиндра она рассчитывается l=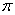 d/2.
d/2.
Для интенсивности процесса испарения со слоя сферических частиц, которые находятся в неподвижном состоянии, в фильтрующийся через слой сушильный агент установлено
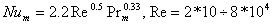 |
(1.11) |
Здесь диаметр сфер является определяющим размером. Скорость воздуха относится к полному сечению установки.
Есть и другие способы обработки полученных экспериментальных данных:
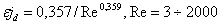 |
(1.12) |
здесь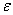 - пористость слоя частиц,
- пористость слоя частиц,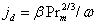 - это фактор массопередачи и
- это фактор массопередачи и ![]() - скорость агента сушки.
- скорость агента сушки.
Разные авторы предлагают различные уравнения для псевдоожиженного слоя, с поверхности частиц которых испаряется влага. Для диапазона Re=5?120 и 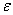 <0.84 предлагается:
<0.84 предлагается:
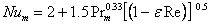 |
(1.13) |
Есть еще ряд соотношений:
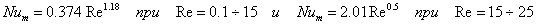 |
(1.14) |
Материал подготовлен по книге: В.Ф.Фролов. Моделирование сушки дисперсных материалов. Издательство "Химия" Ленинградское отделение, 1987 г, 208 с.

 Сушилки для пищевой
Сушилки для пищевой