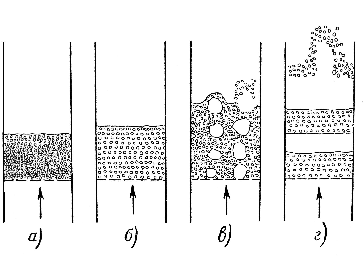
Рассмотрим свойства сыпучих материалов в псевдоожиженном слое, от которых зависит гидродинамика кипящего слоя. Данная технология (псевдоожиженного слоя) применяется не только в химической, фармацевтической и нефтехимической промышленности, но и в технологических процессах пищевой промышленности. Исходя из этого, изложенная ниже теория может применяться при описании и расчетах процессов сушки пищевых продуктов.
Дифференциальная кривая распределения \(\it f(d)\), т.е. плотность вероятностей, и интегральная кривая распределения \(\it F(d)\) характеризуют распределение частиц сыпучего материала с диаметром \(\it d\) и их гранулометрический состав. Функции \(\it f(d)\) и \(\it F(d)\) имеют следующую взаимосвязь:
|
\[\it F(d)=\int_{0}^{d}f(x)dx\] |
(1) |
С помощью функций \(\it f(d)\) и \(\it F(d)\) можно вычислить среднее значение диаметра частиц \(\it M(d)\) и дисперсию случайной величины \(\it d \it \ \sigma_d^2\) - второй центральный момент.
Эквивалентный диаметр \(\it d_{э}\) может быть вычислен различными способами, представленными в таблице 1. От постановки задачи зависит выбор конкретного среднего диаметра. Обычно используют средний гармонический диаметр.
Таблица 1. Способы определения среднего диаметра частиц
| Название | Формула | Примечание |
| Средний арифметический диаметр |
\(\mathit{d_{э}=\dfrac{\sum\limits_{i=1}^n d_{i}n_{i}}{n}=\dfrac{\sum\limits_i^{}\dfrac{g_{i}}{d_i^2}}{\sum\limits_i^{}\dfrac{g_{i}}{d_i^3}}}\) |
\(\it n\) - общее число частиц; \(\it d_{i}\) - средний диаметр частиц \(\it i\) -й фракции; |
| Средний квадратичный диаметр |
\(\it d_{э}=\left(\dfrac{\sum\limits_{i=1}^{n}d_i^2n_{i}}{n}\right)^{1/2}=\left(\dfrac{\sum\limits_{i}^{}\dfrac{g_{i}}{d_{i}}}{\sum\limits_i^{}\dfrac{g_{i}}{d_i^3}}\right)^{1/2}\) |
Суммарная поверхность частиц равна поверхности частицы со средним диаметром, умноженной на число частиц. |
| Средний гармонический диаметр |
\(\it {d_{э}=\dfrac{1}{\sum\limits_{i=1}^{n}\dfrac{y_{i}}{d_{i}}}=\dfrac{\sum\limits_{i}^{}\dfrac{g_{i}}{d_i^3}}{\sum\limits_{i}^{}\dfrac{g_{i}}{d_i^4}}}\) |
\(\it y_{i}\) - счётная доля частиц \(\it i\) -й фракции; Удельная поверхность частиц диаметром \(\it d_{э}\) равна средней удельной поверхности рассматриваемых частиц. |
| Средний диаметр по массе |
\(\it {d_{э}={\sum\limits_{i=1}^n g_{i}d_{i}}=}\left(\dfrac{\sum\limits_{i} n_{i}d^4_{i}}{n}\right)^{1/4}\) |
______ |
Для определения распределения частиц в соответствии с диаметрами применяют методы ситового, седиментационного, микроскопического анализа, а так же пневмовоздушную сепарацию.
Большинство промышленных тонкоизмельчённых сыпучих материалов по дисперсному составу могут быть описаны логарифмически нормальным законом распределения:
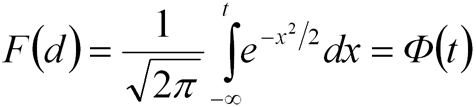 |
(2) |
где 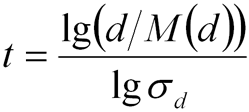 ;
;
![]() - является табулированной функцией.
- является табулированной функцией.
В случае описания свойств материала частиц, имеющих неправильную форму, применяется понятие геометрического коэффициента формы ![]() . Альтернативой ему является обратная величина, которая называется коэффициентом сферичности
. Альтернативой ему является обратная величина, которая называется коэффициентом сферичности ![]() , т.е.
, т.е. ![]() . Коэффициент
. Коэффициент ![]() является отношением поверхности частицы
является отношением поверхности частицы ![]() к поверхности равновеликого шара
к поверхности равновеликого шара ![]() :
:
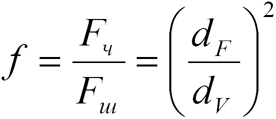 |
(3) |
где ![]() ,
, ![]() диаметры шаров, которые эквивалентны частице по поверхности и по объёму.
диаметры шаров, которые эквивалентны частице по поверхности и по объёму.
Из формулы (3) можно вычислить удельную поверхность несферической частицы:
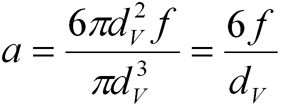 |
(4) |
В тех случаях, когда возникает необходимость учёта отличия формы частицы материала от сферической в большинство формул для кипящего слоя вместо ![]() необходимо подставлять отношение
необходимо подставлять отношение ![]() .
.
В общем случае ![]() ;
; ![]() ; для сферических частиц материала
; для сферических частиц материала ![]() . Коэффициенты
. Коэффициенты ![]() и
и ![]() для тел правильной формы можно найти по таблице 2. Если рассматриваются частицы материала неправильной формы, то значения коэффициентов
для тел правильной формы можно найти по таблице 2. Если рассматриваются частицы материала неправильной формы, то значения коэффициентов ![]() и
и ![]() необходимо определять экспериментально; приблизительную оценку этих коэффициентов можно провести использую таблицу 3. Для совсем грубых расчетов можно пользоваться таблицей 4.
необходимо определять экспериментально; приблизительную оценку этих коэффициентов можно провести использую таблицу 3. Для совсем грубых расчетов можно пользоваться таблицей 4.
Таблица 2. Коэффициенты формы и сферичности некоторых правильных тел
|
Тело |
Тетраэдр | Куб | Октаэдр | Додекаэдр | Икосаэдр | Призма | Цилиндр | |||||||||
| 1,49 | 1,24 | 1,18 | 1,10 | 1,07 | 1,30 | 1,31 | 1,38 | 1,21 | 1,68 | 3,10 | 4,55 | 2,28 |
1,16 | 1,45 | 1,72 | |
| 0,670 | 0,806 | 0,846 | 0,912 | 0,937 | 0,767 | 0,761 | 0,725 | 0,827 | 0,594 | 0,323 | 0,220 | 0,438 | 0,860 | 0,691 | 0,580 | |
Таблица 3. Коэффициенты формы и сферичности некоторых материалов
| Форма частиц материала | ||
| Округлые, окатанные, без резких выступов: глина, шамот, речной песок, короткие цилиндры и пр. | 1,16 – 1,20 | 0,83 – 0,86 |
| Острозернистые, шероховатые, продолговатые: антрацит, неокатанный песок и пр. | 1,54 | 0,65 |
| Песок: | ||
| круглый | 1,20 | 0,83 |
| угловатый | 1,37 | 0,73 |
| остроугольный | 1,67 | 0,60 |
| среднее значение для всех видов песка | 1,33 | 0,75 |
| Вольфрамовый порошок | 1,12 | 0,89 |
| Железный катализатор | 1,73 | 0,58 |
| Активный уголь | ||
| |
1,56 | 0,64 |
| |
1,09 | 0,92 |
| |
1,27 | 0,79 |
| Сланец | ||
| |
2,35 | 0,426 |
| |
1,32 | 0,758 |
| Каменный уголь | ||
| |
1,87 | 0,536 |
| Металлургический кокс | ||
| |
2,48 | 0,403 |
| Гравий | ||
| |
1,47 | 0,68 |
| |
1,38 | 0,725 |
| Пыль | ||
| угольная естественная | 1,54 | 0,65 |
| угольная размельчённая | 1,37 | 0,73 |
| колосниковая оплавленная, сферическая | 1,12 | 0,89 |
| колосниковая агрегированная | 1,82 | 0,55 |
| Слюда (хлопья) | 3,57 | 0,28 |
| Стекло дроблёное, неоплавленное | 1,54 | 0,65 |
| Поливинилхлорид суспензионный | 1,47 | 0,68 |
| Силикагель | 3,03…5,56 | 0,18…0,33 |
| Алюмосиликагель | 1,82…4,0 | 0,25…0,55 |
| Кольца Рашига, сёдла Берля | 3,3 | 0,3 |
| Щебень | ||
| |
1,85 | 0,54 |
| |
1,61 | 0,62 |
| Прокаленный оксид алюминия | 2,32 | 0,43 |
Таблица 4. Оценка коэффициентов формы и сферичности некоторых частиц материалов
| Характеристика формы частицы материала | ||
| Округлые | 1,30 | 0,77 |
| Угловатой формы | 1,52 | 0,66 |
| Продолговатые | 1,72 | 0,58 |
| Пластинчатые | 2,33 | 0,43 |
Надо сказать, что связь геометрического коэффициента формы ![]() и динамического коэффициента формы
и динамического коэффициента формы ![]() имеет корреляции. Причём последний является отношением коэффициента лобового сопротивления несферической частицы к коэффициенту лобового сопротивления сферической частицы, равной ей по объёму:
имеет корреляции. Причём последний является отношением коэффициента лобового сопротивления несферической частицы к коэффициенту лобового сопротивления сферической частицы, равной ей по объёму:
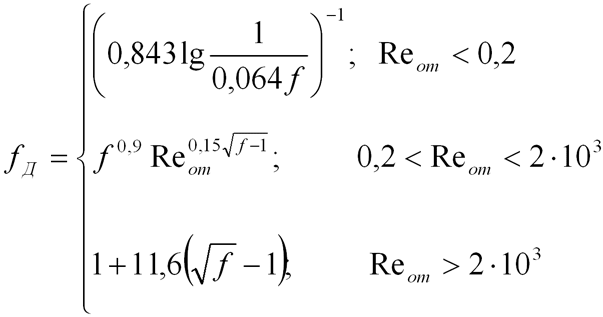 |
(5) |
где ![]() ;
;
![]() - относительная скорость между частицей и газом;
- относительная скорость между частицей и газом;
![]() - кинематическая вязкость газа.
- кинематическая вязкость газа.
Величина ![]() очень важна при проведении расчётов движения частиц в кипящем слое, а также в сепарационной зоне над слоем.
очень важна при проведении расчётов движения частиц в кипящем слое, а также в сепарационной зоне над слоем.
Чтобы охарактеризовать свойства материала частицы или слой частиц применяют понятие прозорности и плотности. При этом разделяют понятие кажущейся плотности частиц ![]() и понятие насыпной плотности слоя частиц
и понятие насыпной плотности слоя частиц ![]() , где
, где ![]() и
и ![]() - масса и объём частиц материала, включающих поры;
- масса и объём частиц материала, включающих поры; ![]() - объём насыпного слоя частиц материала.
- объём насыпного слоя частиц материала.
Довольно часто применяется понятие прозорности слоя ![]() . Она представляет собой долю объёма пустот между частицами в общем объёме слоя. Связь прозорности насыпного слоя
. Она представляет собой долю объёма пустот между частицами в общем объёме слоя. Связь прозорности насыпного слоя ![]() с насыпной плотностью слоя
с насыпной плотностью слоя ![]() выражается формулой
выражается формулой ![]() . Для описания процесса расширения неподвижного слоя с переходом его в кипящий слой можно воспользоваться понятием относительной прозорности
. Для описания процесса расширения неподвижного слоя с переходом его в кипящий слой можно воспользоваться понятием относительной прозорности ![]() . Данный параметр характеризует увеличение доли пустот в процессе псевдоожижения относительно неподвижного слоя:
. Данный параметр характеризует увеличение доли пустот в процессе псевдоожижения относительно неподвижного слоя: ![]() , где
, где ![]() - объём кипящего слоя,
- объём кипящего слоя, ![]() - прозорность кипящего слоя.
- прозорность кипящего слоя.
При подготовке данной темы о свойствах сыпучих материалов использовались данные из книги «Расчеты аппаратов кипящего слоя» под редакцией И.П. Мухленова, Б.С. Сажина, В.Ф. Фролова, 1986 г.

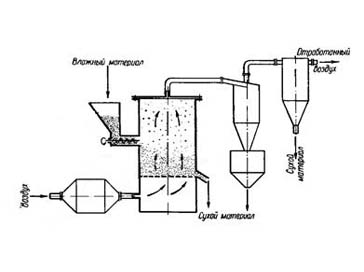
 Сушилки для пищевой
Сушилки для пищевой