Расчёт диска распылительной сушилки

В распылительных сушилках рабочими элементами являются либо форсунки, либо диски, имеющие сложный профиль.

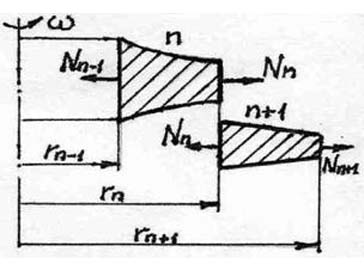
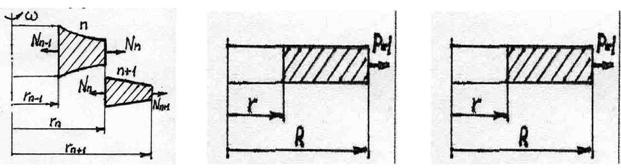
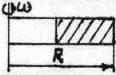
Рассмотрим расчет диска распылительной сушилки. Для этих целей можно воспользоваться методом трех усилий. Выберем смежные участки n и (n+1) (рис. 1). В этом случае радиальные усилия, которые приходятся на единицу длины окружности, составляют:

Участок n: N_n-1  для внутреннего контура и N_n  для наружного контура.
Участок n+1: N_n  для внутреннего контура и N_n+1 для наружного контура.

Учитывая, что радиальные перемещения в сечении двух смежных участков равны, то можно написать для данных участков условия совместной работы.

,

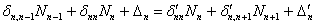здесь 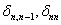  - радиальные перемещения внешнего контура участка n под влиянием на него единичных радиальных усилий, которые приложены к внутреннему и внешнему краям этого участка;

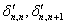  - радиальные перемещения внутреннего контура участка (n+1) под влиянием на него единичных радиальных усилий, которые приложены к внутреннему и внешнему краям этого участка;

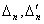  - радиальные перемещения внешнего контура  участка n и внутреннего контура (n+1) участка, спровоцированные влиянием центробежных сил инерции на распылительный диск.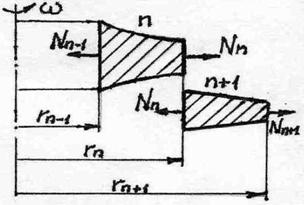

Рис. 1

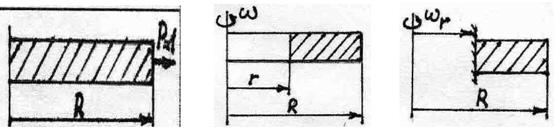
Единичные перемещения 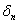находят так. Предположим, что к  внутренней части диска приложена сила Н=1. Чтобы определить перемещение внешнего края используют уравнения:

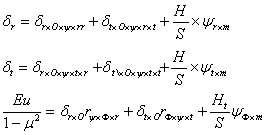
Теперь найдем 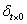, приняв, что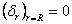

,

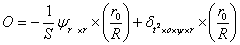из него непосредственно находится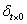

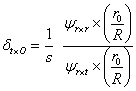
Учитывая последнее уравнение, получим:

Аналогично рассчитывается и перемещение наружного края.

Далее для расчета диска распылительной сушилки необходимо определить перемещение в радиальном направлении края диска под действием сил инерции находят из формул:

В них входят формулы перемещений, которые указаны ниже.

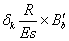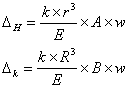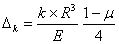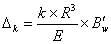Уточнение: символами 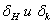обозначаются перемещения в начале и  в конце выбранных участков, которые возникли из-за радиальных усилий;

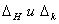обозначаются перемещения в начале и  в конце выбранных участков, которые возникли из-за сил инерции;

Е – модуль продольной упругости, МПа,
s – стандартно обозначаемая толщина диска распылительной сушилки, м;

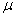– коэффициент Пуассона;

А – коэффициент для начала участка;
В – коэффициент для конца участка;
a и b – индексы, которые указывают на место, куда были приложены усилия;

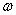– индекс, являющийся показательным для инерционного воздействия, 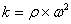(в данном случае 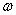- угловая скорость, м/с).

Теперь из всего вышеуказанного можно получить:

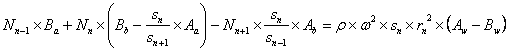
Уравнения для определения коэффициентов будут выглядеть следующим образом:

В каждой формуле имеется по три неизвестных.

После того как определены радиальные усилия, находят радиальные и окружные напряжения. Сначала определяют напряжения при средней толщине выбранных участков.

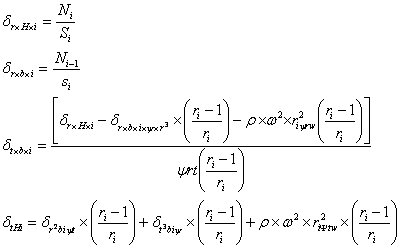
здесь 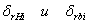- радиальное напряжение;

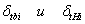- окружное напряжение.

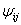- сопровождающие функции.

 
Далее нужно выровнять напряжения в сечениях, в которых в действительных дисках нет резких колебаний толщины материала.

Повторно определяем радиальное напряжение путем деления радиальных усилий на толщину диска в выбранных сечениях.

Чтобы выровнять окружные усилия используется формула:

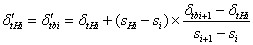
Материал подготовлен по книге "ОБОРУДОВАНИЕ ДЛЯ СУШКИ ПИЩЕВЫХ ПРОДУКТОВ", О.В. Чагин, Н.Р. Кокина, В.В. Пастин : Иван. хим. - технол. ун-т.:Иваново. 2007. 138 с.  и другим источникам.