Модель массообмена

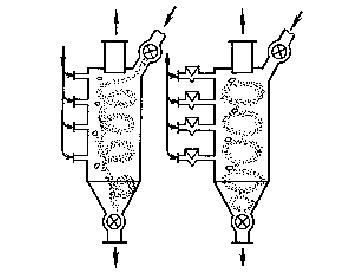
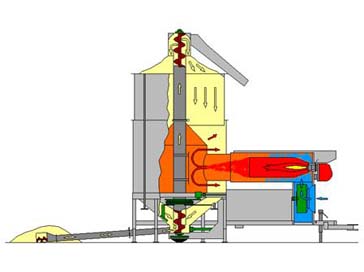
Одни методы расчетов основываются на уравнениях теплообмена, а другие на уравнениях массообмена между потоком агента сушки и поверхностью влажных тел. В одном из источников рассматривается сушка дисперсных материалов в слое, который непрерывно перемещается в поперечном направлении направлению движения агента сушки, и в неподвижном слое. В обоих рассматриваемых случаях диффузионный влагоперенос в направлении движения материала считается пренебрежимо малым и принимается режим вытеснения по агенту сушки, поэтому в результате их анализа получаются одинаковые расчетные соотношения.

За основу кинетики межфазного обмена следует принять уравнение адиабатической сушки, когда движущая сила этого процесса соответствует разности влагосодержаний сушильного агента (Y_w), которая вычислена при температуре мокрого термометра, и влагосодержания основной части агента сушки (Y_G):

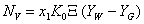(1)

где N_V – скорость сушки, отнесенная к единице поверхности материала; х₁ – относительная скорость сушки; 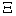- переводной коэффициент между значениями влагосодержаний агента сушки и материала; К₀ – коэффициент массообмена.

Вместе с уравнением (1) необходимо рассмотреть уравнение баланса по удаляемой влаге для потока агента сушки и материала:

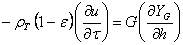(2)

здесь u – влагосодержание материала в расчета на сухую массу.

Через уравнение скорости сушки материала N_V выражается испарение (убыль) влаги из материала:

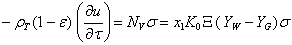(3)

Введем комплексные переменные 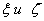, а также искомые функции Ф и П. Благодаря этому система уравнений (2) и (3) приобретает компактный вид:

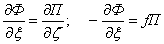(4)

где 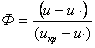- относительное избыточное влагосодержание материала; 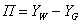- потенциал сушки; 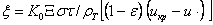- относительное текущее время сушки; 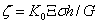- относительная текущая высота внутри слоя материала.

Представленная система (4) эквивалентна:

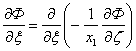(5)

В результате интегрирования этого уравнения по 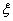получается промежуточный результат:

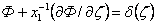(6)

В уравнении (6) 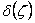- произвольная функция переменной 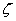. Эта функция определяется из условий равномерного распределения количества влаги в исходном материале по высоте слоя (Ф₀) в начальный момент сушки и соответствующего значения производной 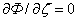в начале процесса: .

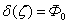Получается:

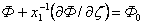(7)

Возможность интегрировать данное уравнение определяется видом связи х₁(Ф). При зависимости общего вида интегрирование может быть проведено численными методами.

Аналитическое решение уравнения (7) получается самым простым при х=1. Это значение х соответствует сушке частиц в периоде с постоянством скорости, значение которой определяется локальным значением температуры агента сушки. В результате получается:

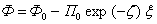(8)

Этот результат аналогичен уже рассмотренному выше для сушки в первом периоде при лимитирующем процессе внешней теплоотдачи.

Окончание первого этапа сушки, когда по всему слою сушка частиц осуществляется в первом периоде, соответствует моменту, когда нижний слой частиц достигает единичного значения влагосодержания 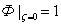. Подставив данное условие в уравнение (8), можно получить время окончания первого этапа процесса сушки:

,

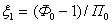здесь П₀ - постоянное во времени значение потенциала сушки на входе агента сушки в слой материала.

После наступления момента 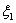нижний слой частиц сушится при значении влагосодержания ниже критического, т.е. величина коэффициента х₁ отличается от единицы. Вверх по слою будет перемещаться фронт, где значение влагосодержания частиц уже равно u_кр. Для распределения влагосодержания по высоте в нижней зоне слоя в пределах до достижения его критического значения аналитическое решение можно получить при предположении линейной зависимости скорости процесса сушки от текущего влагосодержания материала в области второго периода сушки, т.е. когда х=Ф. Тогда при интегрировании уравнения (7) получается:

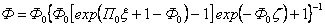(9)

Определить положение фронта критического влагосодержания 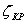можно из уравнения (9) путем подстановки туда :

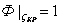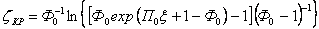(10)

Перед фронтом критического влагосодержания в верхней зоне сушка частиц происходит в периоде с постоянством скорости, которая зависит от локального значения температуры агента сушки. В результате интегрирования уравнения (7) при х₁=1 и 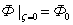в пределах 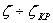получается:

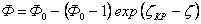(11)

Учитывая принятые допущения, таким образом удается полностью решить задачу определения нестационарных профилей влагосодержания материала по высоте стационарного слоя. Рассчитать средние значения влагосодержания материала по всему слою можно путем интегрирования уравнений (8), (9), (11) по высоте соответствующих зон.

Структура рассмотренных соотношений, которые получены исходя из исходного уравнения массообмена (1), по многим моментам совпадает с соответствующими соотношениями, выведенными исходя из уравнений теплоотдачи.

Для рассмотренной здесь модели массообмена очень важным является факт отсутствия учета меняющейся в зависимости от высоты слоя тепловой обстановки, а в частности неучтение теплоты нагрева высушиваемого материала.  В данном случае были получены аналитические результаты для самых простых случаев – сушки в периодах линейно убывающей и постоянной скорости сушки. В промышленной практике имеются и более сложные кривые процесса. Для них рекомендованы численные методы решения основного уравнения (7). Чтобы по предложенным соотношениям провести расчеты, нужно в результате предварительных опытов найти коэффициент К₀ и .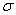

Материал подготовлен по книге: В.Ф.Фролов. Моделирование сушки дисперсных материалов. Издательство "Химия" Ленинградское отделение, 1987 г, 208 с.